以前、CR移相発振回路の発振条件、位相を計算してみました。
今回は、前回の位相計算を4端子定数(4端子パラメータ)で計算してみたいと思います。
「CR移相発振回路を計算してみた」 の計算結果を使いますので、まずは読み直していただくのが良いかなぁと思います。
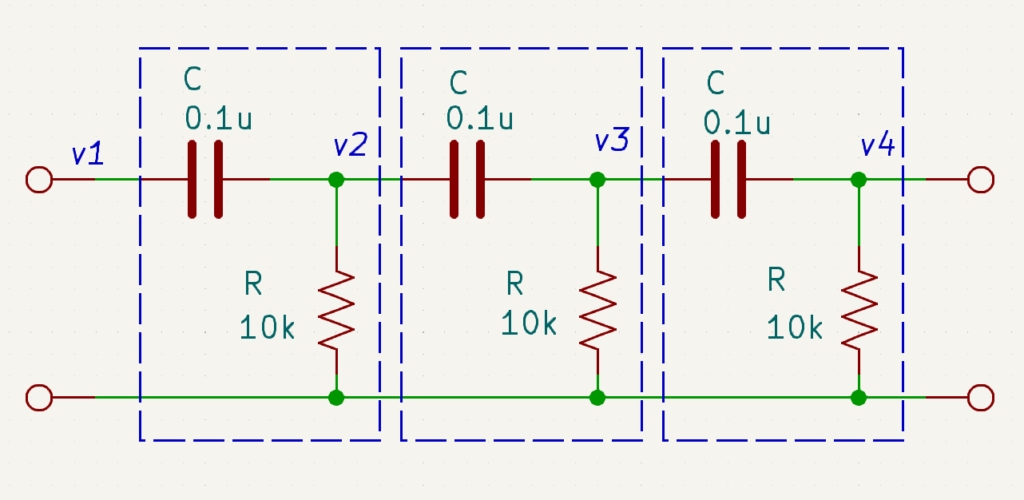
CR移相回路の部分を抜き出しました。
v1が増幅回路の出力に、v4が増幅回路の入力に接続されています。
「増幅回路の入力インピーダンスは十分に高く、出力インピーダンスは十分に低い」ものとします。(回路図は使い回しなので値は気にしないでください)
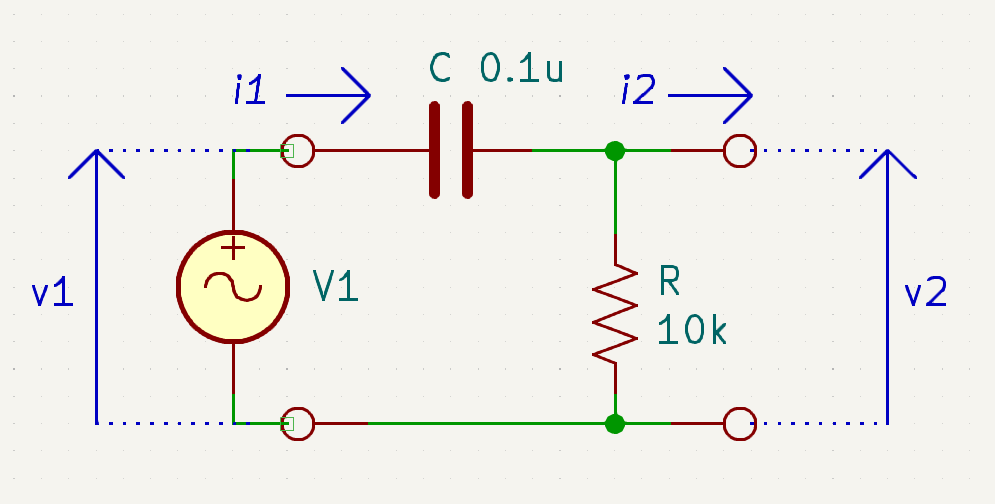
このCR移相回路が三段に接続されています。
$$\begin{align} v1, i1 と v2, i2 の関係は、\\
&\begin{bmatrix}v_1 \\ i_1\end{bmatrix} = \begin{bmatrix}a & b \\ c & d \end{bmatrix}
\begin{bmatrix} v_2 \\ i_2 \end{bmatrix} で表せ、\\
\frac{1}{2\pi f C} = \frac{1}{\omega C} = X とおくと、\\
&\begin{bmatrix}a & b\\ c & d\end{bmatrix}
=
\frac{1}{R}\begin{bmatrix}
R -jX & -jRX\\
1 & R
\end{bmatrix} \\
&でした。
\end{align} $$
また、発振条件(発振しているとき)は、\( X = \sqrt{6}R \) なので、
$$\begin{align}\begin{bmatrix}a & b\\ c & d\end{bmatrix}
&=
\frac{1}{R}\begin{bmatrix}
R -j\sqrt{6}R & -jR^2\sqrt{6}\\
1 & R
\end{bmatrix}
= \begin{bmatrix}
1 -j\sqrt{6} & -jR\sqrt{6}\\
\frac{1}{R} & 1
\end{bmatrix}
\end{align} となります。$$
さて、\(v_1, v_4\)のどちら側から計算するか?ですが、後段のインピーダンスの影響を考慮しないといけないので、後段のインピーダンスが無視できる(=ハイインピーダンス or 開放) \( v_3 – v_4 \)間から計算します。(増幅回路の入力インピーダンスは十分に高いとしたためです)
\( v_3\)と\(v_4\)の位相\( \theta_{3-4} \)を求める
$$
\begin{align}\begin{bmatrix}v_3 \\ i_3\end{bmatrix} = \begin{bmatrix}a & b\\ c & d\end{bmatrix}\begin{bmatrix}v_4 \\ i_4\end{bmatrix}
=
\begin{bmatrix}
1 -j\sqrt{6} & -jR\sqrt{6}\\
\frac{1}{R} & 1
\end{bmatrix}
\begin{bmatrix}v_4 \\ i_4\end{bmatrix}
\end{align}$$
\(v_4, i_4\)側はインピーダンスが十分に高いので開放と同じと考えます。つまり、\(i_4 = 0\)です。
\(v_3とv_4\)の関係は、
$$ v_3 = a\cdot v_4 + 0\cdot i_4= (1-j\sqrt{6}) v_4 \\
よって、
\frac{v_3}{v_4} = 1-j\sqrt{6} です。
$$
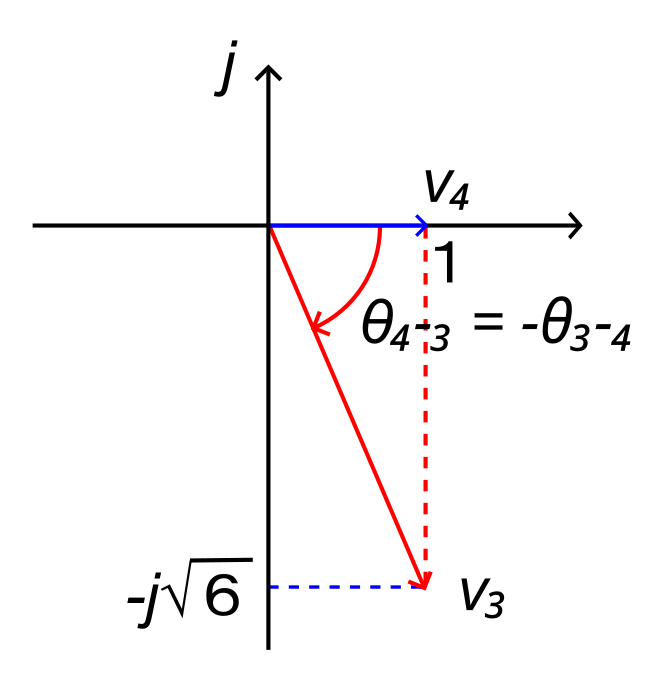
\( 1- j\sqrt{6} \)を複素座標で表すと、このようになります。\( v_4\)を基準とすると、\(v_3\) は\( \theta_{4-3} \)位相が遅れていることになります。
$$ \begin{align} \theta_{4-3} &= \arctan{\frac{-\sqrt{6}}{1}} [rad]\\
&= \frac{180}{\pi}\arctan{(-\sqrt{6})} [^\circ]\\
& \approx -67.79 [^\circ] です。\end{align}$$
\(v_3\)を基準にすると、
$$ \theta_{3-4} = – \theta_{4-3} \approx 67.79[^\circ]です。$$
\( v_2\)と\(v_3\)の位相\( \theta_{2-3}\)、\( v_1\)と\(v_2\)の位相\( \theta_{1-2}\)を求める
直接\(v_2\)と\(v_3\)の位相\(\theta_{2-3}\)を求めようとすると、後段のCR回路のインピーダンスを考慮しないといけないので、\(v_2\)と\(v_4\)の位相\( \theta_{2-4}\)を求めて、\(v_3\)と\(v_4\)との位相\(\theta_{3-4}\)との差をとることにします。
$$
\begin{align}\begin{bmatrix}v_2 \\ i_2\end{bmatrix} &= \begin{bmatrix}a & b\\ c & d\end{bmatrix}\begin{bmatrix}a & b\\ c & d\end{bmatrix}\begin{bmatrix}v_4 \\ i_4\end{bmatrix}
=
\begin{bmatrix}
a^2 + bc & (a+d)b\\
(a+d)c & bc + d^2
\end{bmatrix}
\begin{bmatrix}v_4 \\ i_4\end{bmatrix} \\
&ただし、\begin{bmatrix}a & b\\ c & d\end{bmatrix} = \begin{bmatrix}
1 -j\sqrt{6} & -jR\sqrt{6}\\
\frac{1}{R} & 1
\end{bmatrix}
\\ &i_4 = 0 なので、\\
&v_2 = (a^2 + bc)v_4 = (-5 -j3\sqrt{6})v_4\\
&\frac{v_2}{v_4} = -5 -j3\sqrt{6}
\end{align}$$
$$ \begin{align} \theta &= \arctan{\frac{-3\sqrt{6}}{-5}} [rad] \\
&= \frac{180}{\pi}\arctan{\frac{-3\sqrt{6}}{-5}} [^\circ] \approx 55.77[^\circ]\\
\end{align}
$$
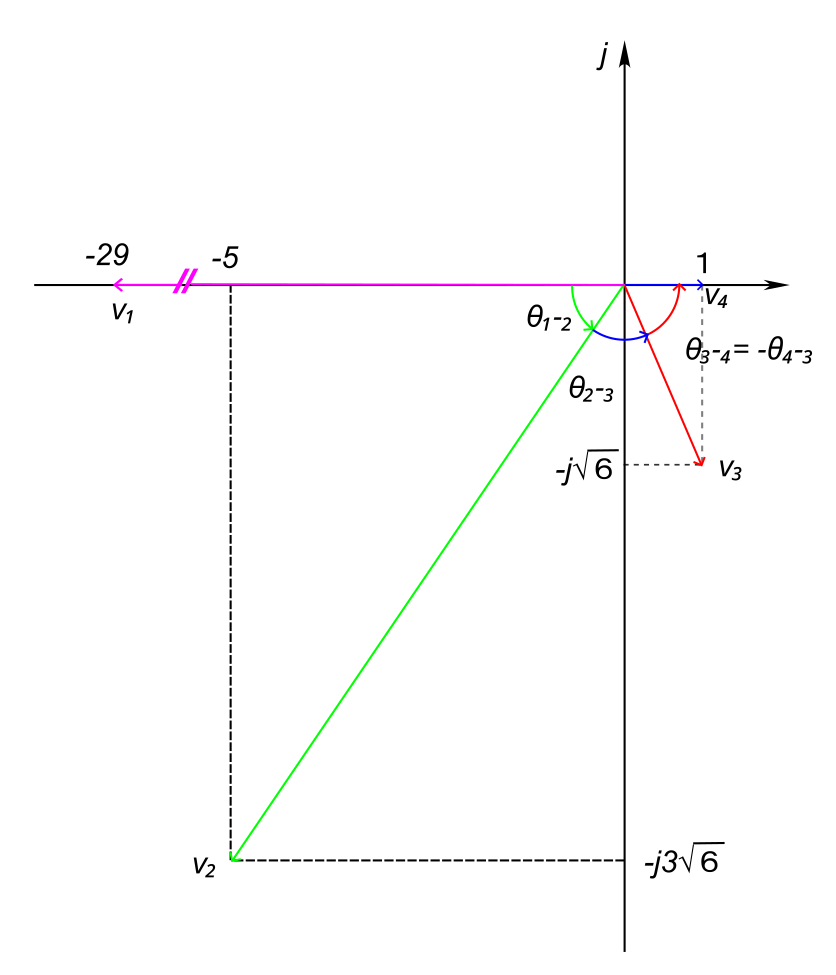
\(\theta = 55.77 [^\circ]\)となりましたが、これは左図をみるとわかるように、実は\(\theta_{1-2}\)と同じなのです。
\( \theta = \arctan{x} \)は、\( -90 \lt \theta \lt 90 [^\circ]\)の間の値を返します。
つまり\(\theta_{2-4} \le -90 \)となったので、正の値(角度)となったのです。
よって、
$$ \begin{align} \theta_{2-3} &= 180 – \theta_{1-2} -\theta_{3-4}\\
&\approx 180 -55.77 – 67.79 = 56.44 [^\circ]
\end{align}$$
当然ながら、結果は以前計算したものと同じになりました。
$$ \begin{align} \theta_{1-2} &= 55.77 [^\circ]\\
\theta_{2-3} &= 56.44 [^\circ]\\
\theta_{3-4} &= 67.79 [^\circ] \end{align}$$
位相は基準を入力側(\(v_1\))を基準にするのか、出力側(\(v_4\))を基準にするのかで、「進み」か「遅れ」が変わってきます。各ベクトルの長さ(大きさ)を比較すると振幅の減衰量もわかりますね。