以前、CR移相発振回路の発振周波数と発振条件を計算してみましたが、その後ネットで移相回路で60°ずつ移相がずれて3段で180°ずれると書かれているのを見かけました。
実際には、後段のインピーダンスの影響をうけるので、同じCRの値で移相回路を構成した場合は、各段60°ずつずれるのではなく、おそらく1段目では60°以下、2段目では60°付近、3段目では60°以上ずれてトータルで180°ずれることになるだろうと思われます。
まぁ、だいたい60°ということであれば間違ってはいないと思いますが、今回は各段でどれぐらい位相がずれるのかを計算してみます。役に立たない計算ですが(笑)
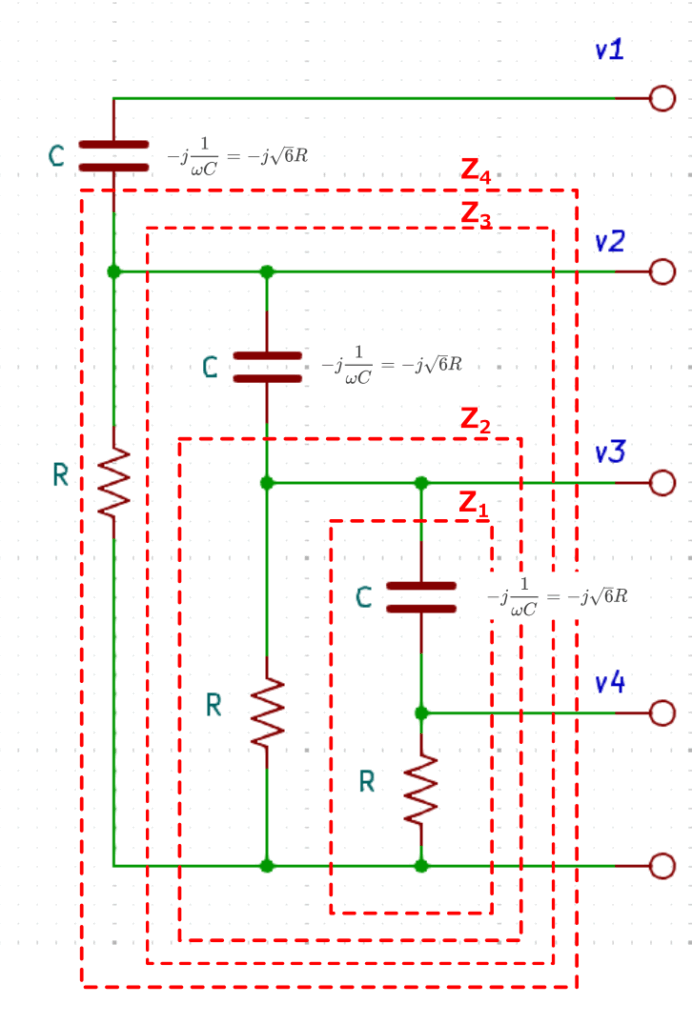
移相回路を書き直してみました。
前回の計算から Cのインピーダンス(リアクタンス)は$$-j\frac{1}{\omega C} = -j \sqrt{6}R $$です。
各段のCRで順に分圧されている回路です。\(v_1\)と\(v_2\)、\(v_2\)と\(v_3\)、\(v_3\)と\(v_4\)の関係(分圧比)を計算すれば、各段での位相変化を求めることができます。
まずは、\(Z_1\)のインピーダンスです。
$$Z_1 = R -j\frac{1}{\omega C} = R – j\sqrt{6}R = R(1-j\sqrt{6})$$
分圧比を計算するので共通の\(R\)を\(R=1\)とし、
$$Z_1 = 1-j\sqrt{6} \tag{1}$$ として計算することにします。
\(Z_2\)は \(R=1\)としたので１と\(Z_1\)の並列(//)です
$$Z_2 = 1 // Z_1 = \frac{ 1-j\sqrt{6}}{1+1-j\sqrt{6}} = \frac{ 1-j\sqrt{6}}{2-j\sqrt{6}} = \frac{8-j\sqrt{6}}{10}\tag{2}$$
\(v_2\)から分圧された\(v_3\)は(2)から、
$$ v_3 = \frac{Z_2}{-j\sqrt{6}+Z_2}v_2 = \frac{\frac{8-j\sqrt{6}}{10}}{-j\sqrt{6} + \frac{8-j\sqrt{6}}{10}} v_2= \frac{13+j8\sqrt{6}}{79} v_2 \tag{3}$$
よって、\(v_2\)と\(v_3\)の位相差\(\theta_{2-3}\)は、
$$ \theta_{2-3} = \arctan{(\frac{8\sqrt{6}}{13})} [rad] = \frac{180}{\pi}\arctan{(\frac{8\sqrt{6}}{13})} [^\circ] \approx 56.44[^\circ]\tag{4}$$
\(Z_3\)は
$$Z_3 = -j\sqrt{6}+Z_2 = -j\sqrt{6} + \frac{8-j\sqrt{6}}{10} = \frac{8- j11\sqrt{6}}{10}\tag{5}$$
\(Z_4\)は
$$Z_4 = 1 // Z_3 = \frac{Z_3}{1+Z_3} = \frac{\frac{8-j11\sqrt{6}}{10}}{\frac{18-j11\sqrt{6}}{10}} = \frac{8-j11\sqrt{6}}{18-j11\sqrt{6}}=\frac{87-j11\sqrt{6}}{105}\tag{6}$$
\(v_1\)から分圧された\(v_2\)は、
$$ v_2 = \frac{Z_4}{-j\sqrt{6}+Z_4}v_1 =\frac{\frac{87-j11\sqrt{6}}{105}}{\frac{87-j116\sqrt{6}}{105}}v_1=\frac{87-j11\sqrt{6}}{87-j116\sqrt{6}}v_1=\frac{5+j3\sqrt{6}}{29}v_1 \tag{7}$$
よって、\(v_1\)と\(v_2\)の位相差\(\theta_{1-2}\)は、
$$ \theta_{1-2} = \arctan{(\frac{3\sqrt{6}}{5})} [rad] = \frac{180}{\pi}\arctan{(\frac{3\sqrt{6}}{5})} [^\circ] \approx 55.77[^\circ]\tag{8}$$
\(v_1\)と\(v_4\)の位相差\(\theta_{1-4} = 180[^\circ]\)なので、\(v_3\)と\(v_4\)の位相差\(\theta_{3-4}\)は、
$$ \theta_{1-4} = \theta_{1-2}+ \theta_{2-3}+ \theta_{3-4} = 180 より\\
\theta_{3-4} = 180 – \theta_{2-3} – \theta_{1-2} \approx 180 – 56.44 – 55.77 \approx 67.79 [^\circ]\tag{9}$$
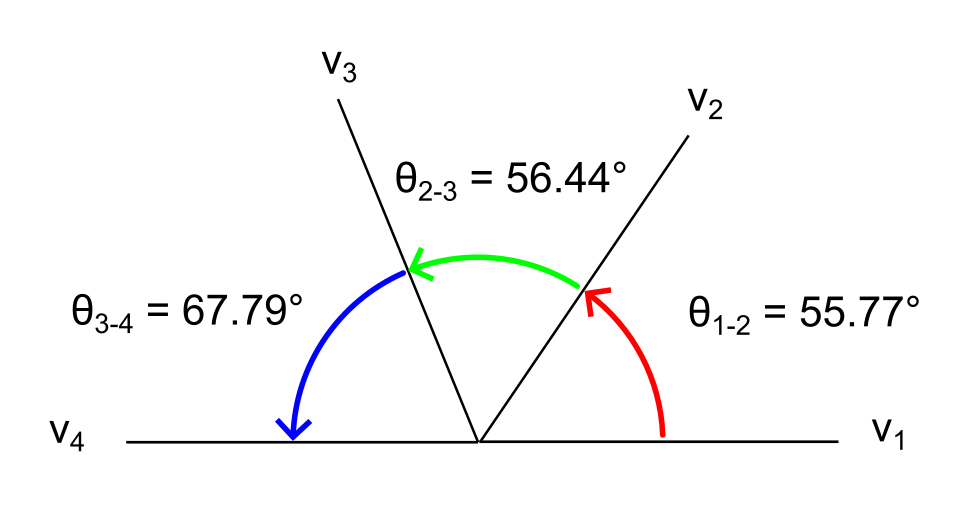
各段の位相はこんな感じですかね。
(振幅は計算していません)
なんとなく2段目はもう少し60°に近いかなと思っていたのですが違いました。
まぁ、計算が間違っているかも知れません(笑)
今回は計算がちょっと面倒くさかったので、Maximaを使って計算してみました。
途中の計算が省略されているのはご勘弁ください(笑)