オペアンプ(反転増幅回路編)

今回は、オペアンプ(OPアンプ)についてです。
オペアンプとは、Operational Amplifiereの略で日本語では演算増幅器と呼ばれています。
なぜ「演算」なのかというと、昔々、アナログコンピュータの演算回路に使われていたからだそうです。さすがに私もアナログコンピュータは使ったことがありません。ほこりにまみれた、真空管式?のアナログコンピュータと思われるものが、スクラップとして廃棄されていたのは見たことがありますが(笑)

アマチュア無線の試験でも、度々オペアンプを使った増幅回路が出題されています。オペアンプ増幅回路の説明は色んなところで解説されていますが、ほとんどが仮想接地、イマジナリーショート/バーチャルショートが前提に説明されています。いきなり、イマジナリーショートといわれても分からない方も多いと思いますので、今回は少し詳しく説明してみたいと思います。電車の中でも読めるように、なるべく省略せずに計算していきたいと思います。

反転増幅回路

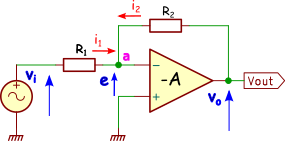
先ずは、理想的なオペアンプを使った反転増幅回路です。入力信号が反転(極性が逆になる)して増幅される回路です。出力の$V_{out}$が$R_2$を介して$-$入力端子に入力(帰還)されている帰還増幅回路です。この増幅回路の電圧利得(増幅率)を求めます。
なお、理想的なオペアンプは、以下の特性をもっているものです。

• 入力インピーダンスが非常に高い(無限大)
• 出力インピーダンスが非常に低い(ゼロ)
• オープンループ電圧利得(ゲイン)が非常に高い(無限大)
• 周波数特性が非常に良い(遮断周波数が無限大)
• その他の特性も理想的

$$\begin{align} 入力信号電圧: &v_{i} [V]\\ 出力信号電圧: &v_{o} [V]\\ 入力抵抗: &R_{1}[\Omega]\\ 帰還抵抗: &R_{2}[\Omega]\\ 差動(誤差)電圧: &e [V] (注)自然対数の底eではありません。\\ オープンループ電圧利得: &-A \end{align}$$

電圧利得

オペアンプは差動増幅回路です。
差動増幅回路は、$+$入力端子と$-$入力端子間の電位差(電圧)$e$ が$A$ 倍増幅され$Vout$に出力されます。
$-$入力端子より$+$入力端子の電位が高いとき、$Vout$は$+$側に増幅されたものが出力されます。
一方、$+$入力端子より$-$入力端子の電位が高いとき、$Vout$は$-$側に増幅されたものが出力されます。
つまり、反転増幅回路では、$-$入力端子と$+$入力端子間の電位差(電圧)を $e$とすると、 オペアンプにより $-A$ 倍増幅され$Vout$に出力されることになります。出力電圧を$v_{o}$とすると、

$$\begin{align} v_{o} &= -A e &と表せます。これを変形すると、\\ -e &= \frac{v_o}{A}&になります。\tag{1} \end{align}$$

$a$点に流れる電流を$i_{1}, i_{2}$とします。オペアンプの$-$入力端子、$+$入力端子とも入力インピーダンスは非常に高く、オペアンプの入力端子にはほとんど電流が流れないと考えます。(実際のオペアンプも、入力インピーダンスは結構高いです)

一方、$a$点の電圧は、$+$入力端子の電圧に対して$e$[V]高いものとします。この回路では、$+$入力端子の電圧はGNDすなわち$0$[V]です。

入力信号$v_{i}$から$R_{1}$を流れる電流$i_{1}$と出力信号$v_{out}$から帰還抵抗$R_{2}$を流れる電流$i_{2}$は、以下の式で表せます。
$$i_{1} = \frac{v_{i}-e}{R_1}\tag{2}\label{1}$$
$$i_{2} = \frac{v_{o}-e}{R_2} \tag{3}\label{2}$$

$-$入力端子には電流が流れないため、$a$点に流れる電流$i_1とi_2$は同じになります。
ここでは、$i_1,i_2$とも$a$点に流れ込む方向としましたから、その和は、 $i_1 + i_2 = 0\tag{4}$になります。
または、流れ込む電流$i_1は、流れ出る電流 -i_2$と同じと考えて$i_1 = -i_2$としても同じです。
$(4)$に$(2)$と$(3)$を代入します。
$$\frac{v_{i}-e}{R_1}+ \frac{v_{o}-e}{R_2} =0 \tag{5}$$
$(5)$を整理します。
$$\begin{align} &通分して、 &\frac{R_2(v_i-e)+R_1(v_o-e)}{R_1 R_2}=0 \\ & 両辺にR_1R_2をかけて、 &R_2(v_i-e)+R_1(v_o-e)=0\\ &展開して、 &R_2v_i+R_1v_o-eR_1-eR_2=0\\ &eでまとめて、 &R_2v_i+R_1v_o-e(R_1+R2)=0 \tag{5′} \end{align}$$

$\displaystyle (1)の -e = \frac{v_o}{A}$を、$(5′)$に代入します。
$$\begin{align} &R_2v_i+R_1v_o-e(R_1+R2) \\ &= R_2v_i+R_1v_o+\frac{v_o}{A}(R_1+R_2) \\ &= R_2v_i+(R_1+\frac{R_1+R_2}{A})v_o = 0 \end{align}$$

これを整理して、
$$v_o = \frac{-R_2}{R_1+\frac{(R_1+R_2)}{A}}v_1 を得ます。$$
この反転増幅器の利得(ゲイン)は、$\displaystyle G = \frac{v_o}{v_1}$ ですから、
$$G = \frac{v_o}{v_1} = \frac{-R_2}{R_1+\frac{(R_1+R_2)}{A}} \tag{6}となります。$$
この式が、この帰還増幅回路の利得を表す基本式です。
オープンループ電圧利得$A$が非常に高い(無限大)とすると、$\displaystyle \frac{(R_1+R_2)}{A}$の分母$A$が$\infty$になりますから、この部分は限りなく$0$に近くなります。
従い、(6)は、 $$G = \frac{v_o}{v_1} ≒ \frac{-R_2}{R_1} となります。$$
これが、一般的な反転アンプの電圧利得の式です。
しかし、オープンループ電圧利得が有限な場合は、(6)の式で計算する必要があります。アマチュア無線の試験でもオープンループ利得が有限の問題が出たことがありますので、導出方法を覚えておいても損はないでしょう。

理想オペアンプであれば、最初から$e = 0$として、
$$\begin{align} &i_1 + i_2 = 0 \enspaceから\\ &\frac{v_i-0}{R_1} + \frac{v_o -0}{R_2} = \frac{v_i}{R_1} + \frac{v_o}{R_2} =0\\ &\frac{v_0}{R_2} = -\frac{v_i}{R_1}\\ &\unicode{x2234} \enspace v_o = -\frac{R_2}{R_1}v_i \enspaceと考えるのが早いです。 \end{align}$$
一般のオペアンプを使う場合でも、周波数が低い帯域ではオープンループ電圧利得は十分に高いので、この式を使って計算することがほとんどです。しかし、周波数が高くなってくるとだんだん誤差が大きくなってくることを認識しておきましょう。

イマジナリーショート/バーチャルショート/仮想短絡

$(1)$の式$\displaystyle -e = \frac{v_o}{A}$ は、$-$入力端子と$+$入力端子間の電圧$e$が$-A$倍に増幅されて、出力$v_o$になるという関係式を変形したものです。
理想的なオペアンプは、オープンループ利得$A$が非常に高いので、$A \rightarrow \infty$とすると、
$$-e = \frac{v_o}{A} \rightarrow \frac{v_o}{\infty} \rightarrow 0 となります。$$
$e$は、$-$入力端子と$+$入力端子間の差の電圧ですから、$-$入力端子と$+$入力端子が同電位になる、すなわち$-$入力端子と$+$入力端子が短絡したものと同じことになります。
「仮想的に短絡しているとみなせる」ということです。これをイマジナリーショートといいます。昔はイマジナリーショートと言ってましたが、最近はバーチャルショートと言うようですね。

もちろん、実際には短絡しませんので、$-$入力端子から$+$入力端子へ電流が流れるわけではありませんし、$(1)$式からもわかるように、$e=0$では出力も$0$になるので、$-$入力と$+$入力の差が非常に小さくなるということです。

電流$i_1$はどこに流れるかというと、$i_2$として$R_2$を通じて$V_{out}$に流れることになります。$R_2$を経由するわけですから、$R_2 > R_1$の場合は、$v_o$は$v_i$より大きく反対方向に振らないといけないことになります。つまり、$v_i$に対して$v_o$は、反対方向に増幅されるということです。
また、この反転アンプの回路図の$+$入力端子は、GNDに接続されています。GNDに接続することを「接地する」ともいいます。つまり、この反転アンプでは、$-$入力端子は仮想的にGNDに接続されている、「仮想接地」されていることになります。

反転アンプで注意すること

入力インピーダンスは、$R_1$になりますから、入力インピーダンスは、それほど高くできません。
また、反転アンプの電圧利得は、$\displaystyle G = \frac{-R_2}{R_1}$でした。実際のオペアンプでも出力インピーダンスは出力につながれる負荷や、$R_2$に比べても十分小さい場合が多いですが、$R_1$は、入力信号のインピーダンスにも影響されます。つまり、接続される信号の出力インピーダンスによって電圧利得が変動することになるということです。これは、実際の回路を組む時に注意しておく必要があります。

アマチュア無線の試験では、$+$入力端子が無い増幅回路も出題されますが、考え方も結果も同じです。
これは、$e$がGNDからの電圧と考えると、$+$入力端子がGNDに接続されているものと同じだからです。

今回は、オペアンプ(差動アンプ)を使った反転増幅回路の説明でした。
数式を表示するのにMathJax-LaTeXを使ってみました。昔は何でもLaTeXで書いていたのですが、久しぶりに使うとほとんど忘れていました(笑)

次回は、非反転増幅回路の説明をしたいと思います。